Auf Messen und Vor-Ort-Veranstaltungen ist es schwierig den Nutzen und die Funktionsweise von Data Science bzw. Machine Learning zu veranschaulichen. Insbesondere wenn nicht nur auf Theorie zurückgegriffen werden soll.
Aus diesem Grund entstand die Idee einen physischen Prototypen zu schaffen, dessen Daten live mit Maschine Learning Methoden analysiert werden. Wir entschieden uns auf ein bestehendes Modell zurückzugreifen und dieses mit zusätzlicher Sensorik auszustatten.
Inhaltsverzeichnis
1. Datenerhebung – Bau der Sensorik
2. Architektur
3. (Sensor-)Datenverarbeitung
4. Auswertung – Anomalieerkennung
4.1 Arten von Anomalieerkennung
4.2 Verteilungsbasierte Verfahren
4.3 Dichtebasierte Verfahren
4.4 Anomalieerkennung vs. Klassifikation
4.5 Anomalieerkennung für den Bagger Use Case
4.6 Übertragung des Baggers Use Case auf die Realität
Dieser verfügt bereits von sich aus über 7 Motoren, welche einzelne Teile des Baggers bewegen und über eine Smartphone-App gesteuert werden können.
In diesem Blogartikel beschreiben wir, wie ein solches Modell mit zusätzlichen Sensoren ausgestattet werden kann, welche Besonderheiten es bei der Verarbeitung von Sensordaten gibt und wie mit Data MiningWas ist Data Mining?Data Mining ist die computergestützte Verarbeitung sowie… Verfahren eine Echtzeitüberwachung der Sensoren (mit Ausreißer Erkennung) implementiert werden kann.
Datenerhebung – Bau der Sensorik
Die 7 Motoren des Baggers werden über „Hubs“ angesprochen. Diese stellen die Verbindung zur Smartphone-App via Bluetooth her. Um Belastungssituationen zu erkennen, messen wir die, an den Motoren anliegende, Spannung. Die Spannung kann parallel gemessen werden, sodass keine der bestehenden Verbindungen aufgetrennt werden musste. Stattdessen wurden dünne Drähte an die Kontaktstellen gelötet.
Diese Drähte leiten die Spannung zu einer Platine, welche mit einem ESP8266 bestückt ist. Der ESP8266 ist ein ein Platinen-Chip mit WLAN-Modul und kann programmiert werden. Der ESP8266 liest untersekündlich die anliegenden Spannungen aus.
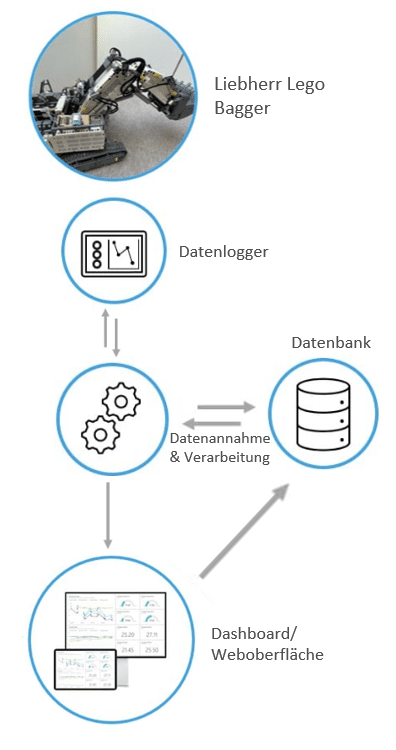
Architektur
Über WLAN werden die ausgelesenen Spannungen an einen Endpunkt zur Datenannahme geschickt. Dieser führt mehrere Aktionen durch:
- Bringt die Daten in eine zeitliche Reihenfolge.
Der ESP8266 verfügt über keine Uhr und kann somit keinen Zeitstempel zu den Sensordaten mitliefern. Das IP-Protokoll sieht keine strikte Reihenfolge der Datenpakete vor. Es kann also sein, dass eine spätere Messung vor der vorherigen Messung eintrifft. Um dieses Problem zu umgehen, sendet der ESP8266 einen hochzählenden Counter mit, damit die Messungen darauf basierend in Reihenfolge gebracht werden können. - Legt die Messungen in der Datenbank ab, damit eine Historie vorliegt, welche mit Maschine Learning analysiert und Modell darauf trainiert werden kann.
- Führt eine Anomalieerkennung durch. In diesem speziellen Fall haben wir uns für eine Ausreißer Analyse (engl. Anomaly Detection) entschieden. Damit die Ergebnisse dieses Modells genutzt werden können, muss es auf neu eintreffende Daten angewandt werden.
- Leitet die Daten weiter an das Dashboard, damit diese möglichst schnell sichtbar werden und ggfs. ein Nutzer/Operator handeln kann.
(Sensor-)Datenverarbeitung
Bei der Erhebung und Auswertung gibt es einige Punkte, die (insbesondere für den Data Scientisten) zu beachten sind.
Sensordaten kommen in der Regel als Stream, also als kontinuierlicher Datenfluss, rein und werden dann mit Zeitstempel und Bezug zum Sensor abgelegt. Damit ist eine eindeutige Zuordnung zur Maschine vorhanden. Allerdings lassen sich andere Daten wie Stamm-, Auftrags oder Wartungsinformationen oft nur über die Kombination „Maschine und Zeitstempel bzw. Zeitabschnitt“ zuordnen. Die zeitlichen Komponenten spielt in den „klassischen“ Systemen einer eher untergeordneten Rolle – ob eine Störung bspw. 10min später oder früher aufgetreten ist, ist bei der Abwicklung der Störungsbeseitigung nebensächlich.
In 10min können hingegen tausende Sensorpunkte eintreffen, die dann fälschlicher Weise als „Störung“ bzw. gegenteilig klassifiziert werden. Dies macht eine spätere Auswertung sehr schwierig. Indem die Sensoren selbst mit einbezogen werden lässt sich dieses Problem lösen. Wenn eine Anlage eine Störung hat, dann steht diese in der Regel danach und in vielen Fällen gibt es einen Sensor, der eine Indikation gibt, ob die Maschine läuft oder nicht. Entsprechend kann der Störungszeitpunkt als Näherungswert genommen werden und über die Sensorwerte (mit Schwellwerten bspw.) ein exakter Zeitstempel abgeleitet werden.
Ein weiteres Problem von Sensordaten-Strömen ist, dass diese in einem zeitlichen Abschnitt ausgewertet werden sollten. Einige Sensoren tendieren dazu zu schwanken. Dies kann an Ungenauigkeiten des Sensors liegen. Es kann aber auch sein, dass die zu messende Eigenschaft auf natürliche Weise stark variiert.
Ein Beispiel:
Sie haben die Motordrehzahl von vielen Autofahrten und wollen diese vergleichen hinsichtlich Verschleißes. Einige Autofahrer fahren eher gemächlich mit konstanter Geschwindigkeit und andere Autofahrer tendieren dazu immer stark zu beschleunigen und dann wieder abzubremsen. Ein Mensch würde in den Sensorkurven daraus resultierende „Zacken“ schnell erkennen und vermuten, dass der Verschleiß bei dem zweiten Profil höher ist.
Wie lässt sich dies jedoch mit Machine Learning auswerten?
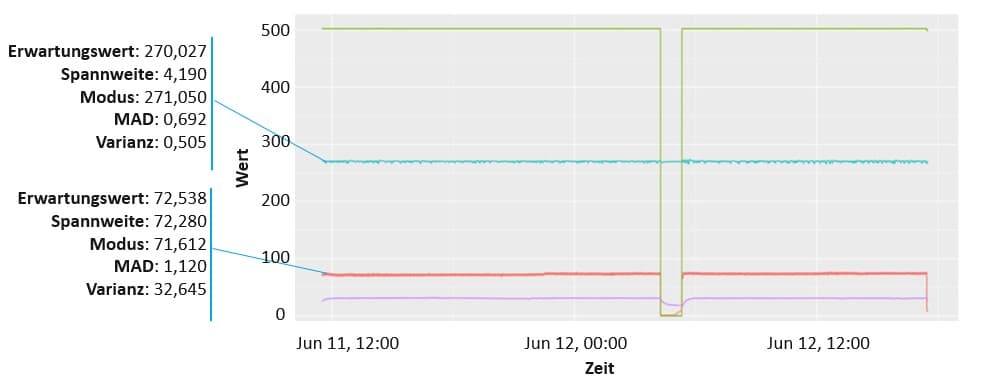
Die durchschnittliche Motordrehzahl kann dann bei allen Fahrten identisch sein. Und besonders hohe und niedrige Drehzahlen finden sich auch in jedem Profil, weil vorausschauende Autofahrer auch mal beschleunigen bzw. bremsen müssen. Wird also ein Modell ohne Vorverarbeitung auf diese Daten angewandt, könnte es im besten Fall lernen, dass hohe Drehzahlen zu einem höheren Verschleiß führen. Dies geschieht aber nur, wenn der Anteil der „sportlichen Fahrweisen“ auch hoch ist. Ansonsten würde dies in der Allgemeinheit untergehen. Zum Glück gibt es eine Reihe von mathematischen Kennzahlen die Sensorkurven, also Sensorwerte im zeitlichen Verlauf, beschreiben können. Damit wird für Machine Learning Algorithmen, das was ein Mensch „auf den ersten Blick“ sieht, auch ersichtlich.
Die Varianz, MAD (Mean Absolut Deviation), AAD (Absolut Average Deviation) sind Beispiele für Kennzahlen die sich bei der „sportlichen Fahrweise“ deutlich zur „moderaten Fahrweise“ unterscheiden würden. Zudem lassen sich mit dieser mathematischen Beschreibung Fahrten unterschiedlicher Länge leicht miteinander vergleichen.
In unserem Use-Case haben wir eine Ausreißer Erkennung implementiert und wegen der Einfachheit der Sensoren auf eine solche Kennzahl verzichtet.
Auswertung – Anomalieerkennung
Anomaly Detection bzw. Anomalieerkennung ist ein Data Mining Verfahren zur Identifikation von ungewöhnlichen Datenpunkten bzw. Beobachtungen, die sich signifikant von der Gesamtheit der Daten unterscheiden. Diese Methode wird verwendet, um u.a. Kreditkartenbetrug sowie System- und Produktionsstörungen zu entdecken. Ein weiterer Anwendungsfall ist die Ermittlung von Ausreißern zur Datenbereinigung.
Arten von Anomalieerkennung
Es existieren zahlreiche Methoden zur Ausreißererkennung. Die geläufigste Unterteilung dieser ist in überwachte, unüberwachte und semi-überwachte Verfahren.
Überwachtes Lernen
Es liegen gelabelte Trainingsdaten zum Erlernen des Modells vor. Das heißt, dass bekannt ist, welche Daten des Trainingsdatensatzes Anomalien sind.
Semi-Überwachtes Lernen
Beim semi-überwachten Verfahren wird ein Modell auf Basis einer Trainingsmenge ohne Anomalien trainiert und die Wahrscheinlichkeit ermittelt, dass ein Datensatz, vom erlernten Modell abstammt.
Unüberwachtes Lernen
Es liegen nicht gelabelte Trainingsdaten zum Erlernen des Modells vor. Das heißt, dass nicht bekannt ist, welche Daten Ausreißer sind. Bei diesen Verfahren wird die Annahme getroffen, dass die meisten Daten keine Ausreißer sind.
Univariate vs Multivariate Verfahren
Neben der Art der Ermittlung des Modells können die Modelle auch nach der Art der Daten- Dimensionalität unterteilt werden. Es existieren univariate Verfahren, die auf eindimensional verteilte Daten angewendet werden, sowie multivariate Verfahren für mehrdimensional verteilte Daten.
Verteilungsbasierte Verfahren
Interquartilsabstand
Bei der Interquartilsmethode wird ein Bereich bzw. eine Range um den Median der Stichprobenmenge herum definiert. Alle Beobachtungen außerhalb dieser Range werden als Ausreißer identifiziert.
GESD (Generlized Extreme Studentized Deviate Test)
Es werden Hypothesentests anhand folgender Teststatistik durchgeführt 
, wobei x_Strich das und sigma die Standardabweichung der Stichprobe darstellt.
Die Nullhypothese ist, dass keine Ausreißer im Datensatz vorliegen. Die Alternativhypothese lautet, dass bis zu r Ausreißer vorliegen. Es werden r Tests durchgeführt, solange die Teststatistik über einen kritischen Wert liegt. Dabei wird nach jedem Test der Datenpunkt mit dem größten Abstand zum arithmetischen Mittel aus der Datenmenge als erkannter Ausreißer entfernt und die Teststatistik neu berechnet.
Dichtebasierte Verfahren
Dbscan
Dbscan ist ein Clustering Verfahren, dass Cluster auf Basis der Dichte ermittelt. Ein Punkt wird als dicht bezeichnet, wenn sich mindestens MinPts Punkte in einer Umgebung mit Radius ɛ um den Punkt herum befinden. Zur Ermittlung des Abstands zwischen Punkten existieren diverse Metriken, wie z.B. die Euklidische Metrik, die verwendet werden können.
Das Verfahren unterscheidet drei Arten von Punkten. Die erste Art von Punkten sind Kernpunkte. Dieses sind Punkte, die dicht sind. Die zweite Art sind dichte-erreichbare Punkte. Diese sind Punkte, deren e-Umgebung weniger als MinPt Punkte enthält, jedoch von einem Kernobjekt des Clusters erreichbar sind. Mit erreichbar ist gemeint, dass der Abstand zwischen zwei Punkten kleiner als e ist. Als drittes existieren Ausreißer. Diese sind Punkte, die nicht dichte-erreichbar sind von anderen Punkten.
Ein Cluster wird folgendermaßen charakterisiert: Alle Punkte des Clusters sind dichte-verbunden. Zwei Punkte werden als dichte-verbunden bezeichnet, wenn es einen Punkt gibt, von dem die beiden Punkte dichte-erreichbar sind. Ist ein Punkt dichte-erreichbar von einem beliebigen Punkt des Clusters, so ist dieser Punkt Teil des Clusters. Somit werden mittels dieses Verfahrens Ausreißer als eigenständige, nicht dichte Cluster identifiziert.
Isolation Forests
Dieses Verfahren basiert auf binären Entscheidungsbäumen. Zum Trainieren eines Entscheidungsbaumes, wird ein Feature willkürlich ausgewählt und eine willkürliche Trennung anhand einer Wert-Ausprägung dieses Features durchgeführt.
Der Isolation Forest ergibt sich dann aus der Kombination aller Isolationsbäume, sodass der Durchschnitt ihrer Ergebnisse verwendet wird.
Jede Beobachtung wird in einem Knoten mit dem Isolationswert verglichen. Die Anzahl der Isolationen wird Pfadlänge genannt. Die Annahme ist, dass Ausreißer kürzere Pfadlängen aufweisen als normale Beobachtungen.
Der Ausreißer-Score wird dann wie folgt bestimmt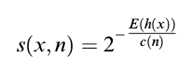 
, wobei h(x) die Pfadlänge von Beobachtung x, c(n) die maximale Pfadlänge des Baumes und n die Anzahl der Knoten des Baumes sind. Der Wert liegt zwischen 0 und 1. Je höher der Wert ist, desto wahrscheinlicher handelt es sich bei der Beobachtung um einen Ausreißer.
K-Nearest Neighbour
Mithilfe des K-Nearest Neighbour Algorithmus lassen sich auch Anomalien identifizieren. Dabei ist die Distanz eines Datenpunkts zum k nächsten Nachbar das Maß für den Ausreißer Score.
Anomalieerkennung vs. Klassifikation
Klassifikation ist ein überwachtes Machine Learning Verfahren zur Klassifizierung von Daten. Dabei wird angenommen, dass die einzelnen Label ähnlich oft vorkommen.
Bei der Anomalieerkennung hingegen wird von einem Ungleichgewicht zwischen normalen und abnormalen Daten ausgegangen. Viele normale Daten stehen wenigen Anomalien gegenüber. Außerdem müssen die Trainingsdaten nicht zwingend gelabelt sein, wie bereits zuvor beschrieben.
Anomalieerkennung für den Bagger Use Case
Für die gemessenen Spannungen wurde die Annahme getroffen, dass diese losgelöst voneinander betrachtet werden können. Außerdem lagen nur ungelabelte Daten vor. Somit ist ein unüberwachtes und univariates Verfahren für die Anomalieerkennung zu verwenden.
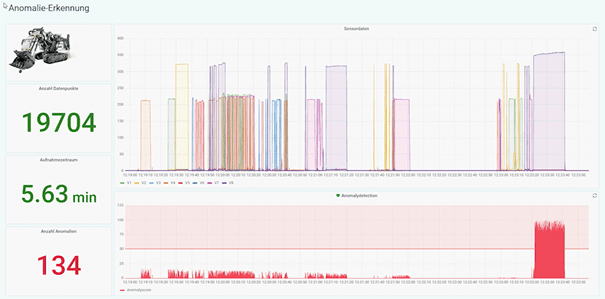
Die Interquartilsmethode weist diese Eigenschaften auf und wurde daher ausgewählt, um die Anomalieerkennung durchzuführen. Die Ergebnisse der Ausreißererkennung sind auf dem unten aufgeführten Bild dargestellt.
Übertragung des Bagger Use Case auf die Realität
Mit diesem Use-Case konnten wir zeigen, wie Sensordaten maschinell überwacht werden können. Die Anomalie war nicht besonders schwer zu erkennen. Jedoch kann ein solcher Algorithmus viele Maschinen gleichzeitig non-Stop überwachen und ggfs. bei Auffälligkeiten Menschen mit einbeziehen.
Dies ist insbesondere im produzierenden Gewerbe interessant. Eine fehlerhafte Produktion kann schnell zu hohen Ausschüssen führen. Mit einer Anomalie-Erkennung kann auch hier ggfs. Zeit bis zum Einschreiten gewonnen werden.
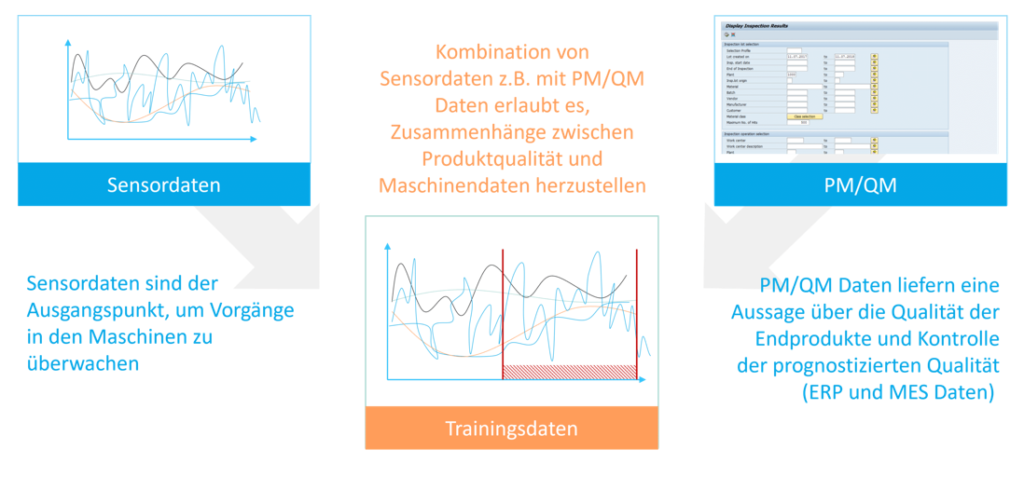
Insbesondere unter Einbeziehung weiterer Datenquellen, wie dem PM (Planned Maintenance) oder dem QM (Qualitäts Management), lassen sich weitere Use-Cases identifizieren.
Mit entsprechenden Methoden können Data Scientisten unter anderem Einflussfaktoren auf Verschleiß oder Qualität identifizieren. Dies wiederum kann genutzt werden, um positiven Einfluss auf diese Faktoren auszuüben oder diese genau zu überwachen.
Autor: Bernd Themann
Kay Rohweder
Senior Manager
SAP Information Management
kay.rohweder@isr.de
+49 (0) 151 422 05 242
